Publications

A full publication list can be found on my Google Scholar.

Selected non-orthogonal configuration interaction with compressed single and double excitations (Link)

C. Sun, F. Gao and G. E. Scuseria. J. Chem. Theory Comput. 20, 9, 3741–3748 (2024).

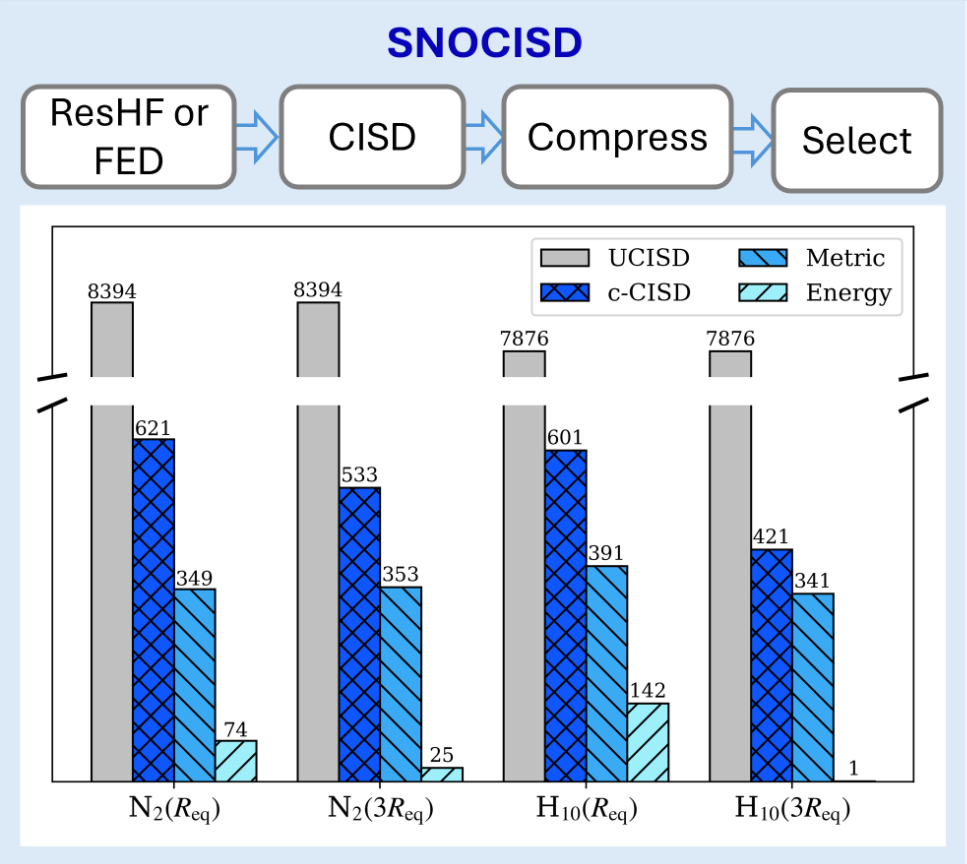
We derived elegant formulae to compress a linear combination of orthogonal particle-hole excitations into a much shorter non-orthogonal configuration interaction (NOCI). We further combine this strategy to add dynamic correlation to an NOCI reference, providing a systematically improvable approach to add arbitrary rank of excitations to a multi-reference wavefunction.

Waveflow: boundary-conditioned normalizing flows applied to fermionic wavefunctions (Link)

L. Thiede, C. Sun (Co-first Author, Corresponding Author), A. Aspuru-Guzik. APL Mach. Learn. 2, 046106 (2024). Featured Article

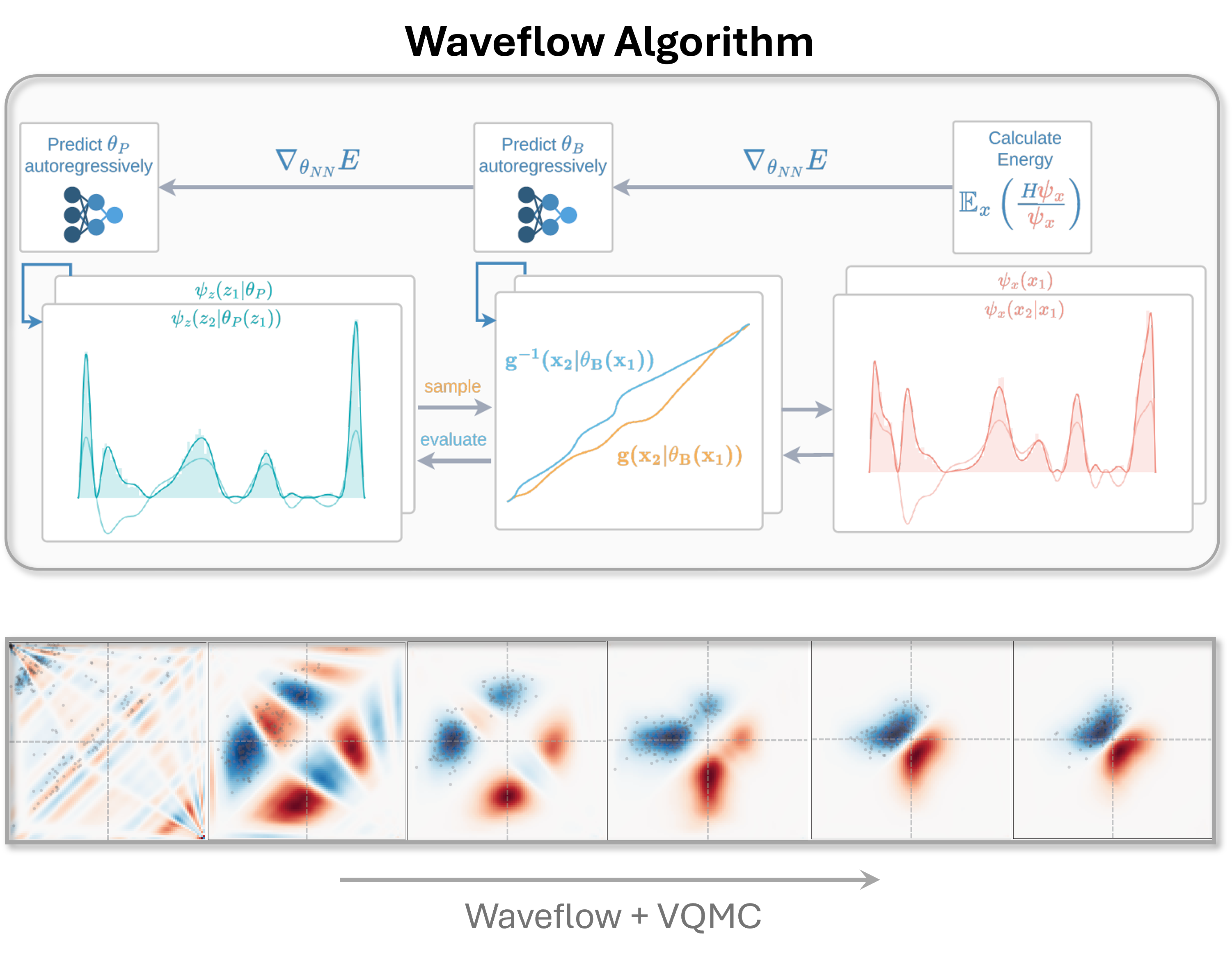
We introduced Waveflow, an innovative framework for learning many-body fermionic wavefunctions with boundary-conditioned normalizing flows. Rather than relying on Slater determinants, Waveflow achieves antisymmetry by defining the wavefunction's fundamental domain and enforcing the appropriate boundary conditions. Furthermore, we introduced a method for relaxing both the prior distribution and the flow, enabling us to overcome the longstanding topological mismatch problem in normalizing flows.

Electron localization in disordered quantum systems at finite temperatures (Arxiv)

C. Sun, arXiv:2403.16868 [cond-mat.dis-nn]

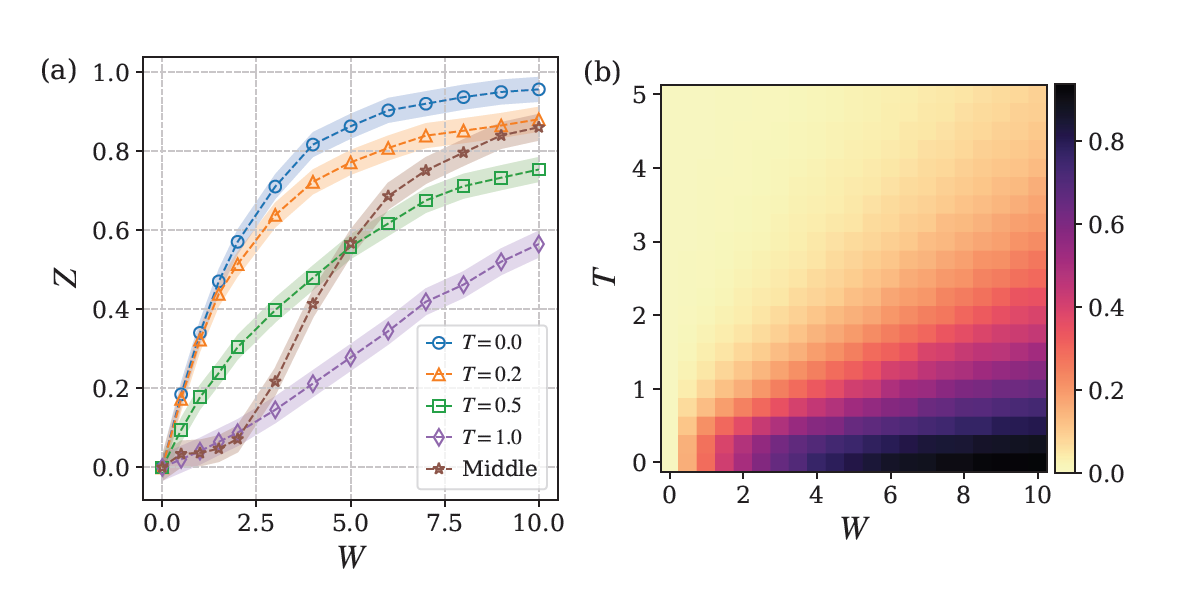
Disordered quantum systems exhibiting many-body localization (MBL) hold promise as noise-resilient materials for quantum computing. In this work, we investigate electron localization within disordered quantum systems, examining both individual eigenstates and thermal states. We use complex polarization as a numerical indicator to characterize the system's localization length. Additionally, we evaluate the effectiveness of the mean-field approximation in delivering a quantitative analysis of these systems.

Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution (Link)

M. Motta, C. Sun, A. T. K. Tan, M. J. O’Rourke, E. Ye, A. J. Minnich, F. G. S. L. Brandão and G. K.-L. Chan. Nat. Phys. 16, 205–210 (2020).

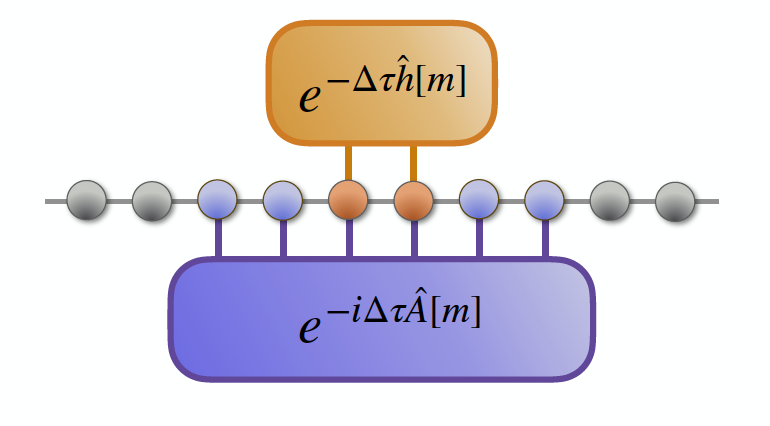
This work provides a quantum algorithm for imaginary time evolution (ITE). The biggest challenge of implementing ITE on a quantum computer is that the ITE operator is non-unitary. Unlike the popular block encoding approach, our algorithm does not require ancillary qubits. The key is to utilize the entanglement pattern of a physical system.

Finite-temperature density matrix embedding theory (Link)

C. Sun (Corresponding Author), U. Ray, Z.-H. Cui, M. Stoudenmire, M. Ferrero, and G. K.-L. Chan. Phys. Rev. B 101, 075131 (2020).

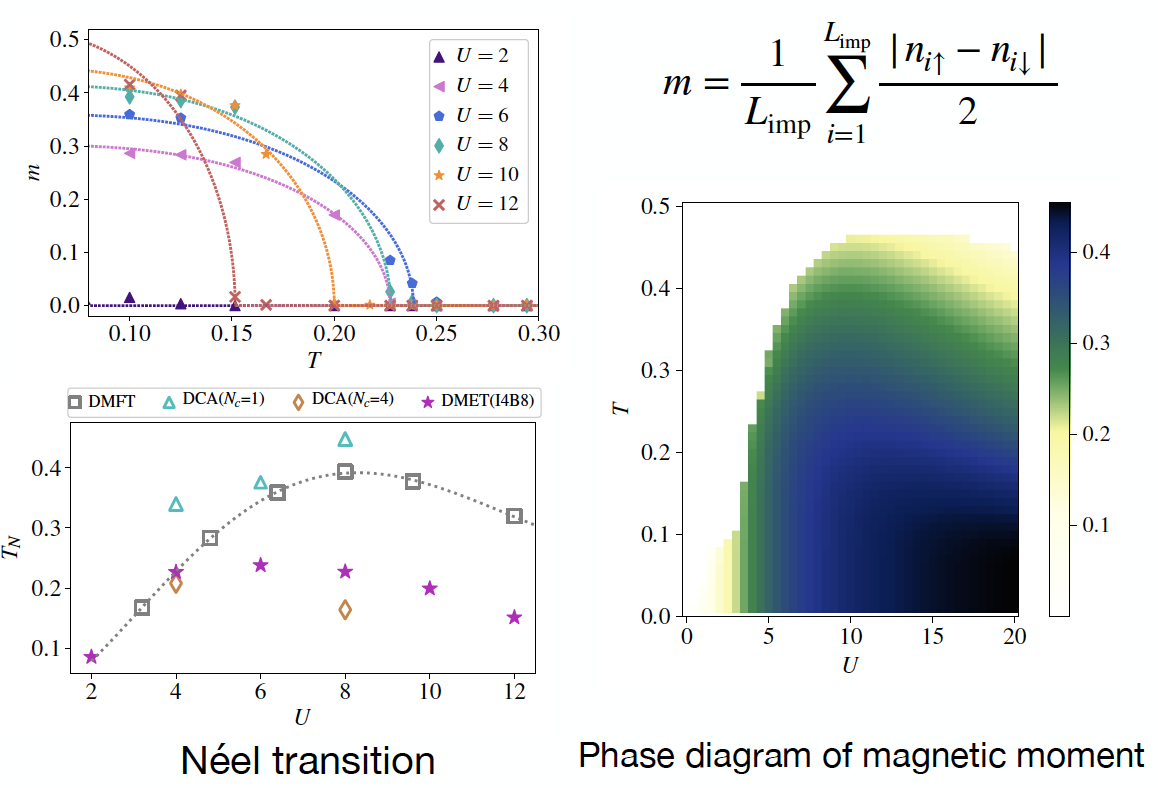
This paper provides a new vision on the behavior of entanglement at finite temperature. It also provides a numerical algorithm called finite-temperature density matrix embedding theory (FT-DMET), which is powerful for computing observables and phase diagrams for strongly correlated systems at finite temperature.

Ground-state phase diagram of the three-band Hubbard model from density matrix embedding theory (Link)

Z.-H. Cui, C. Sun, U. Ray, B.-X. Zheng, Q. Sun, and G. K.-L. Chan. Phys. Rev. Research 2, 043259 (2020).

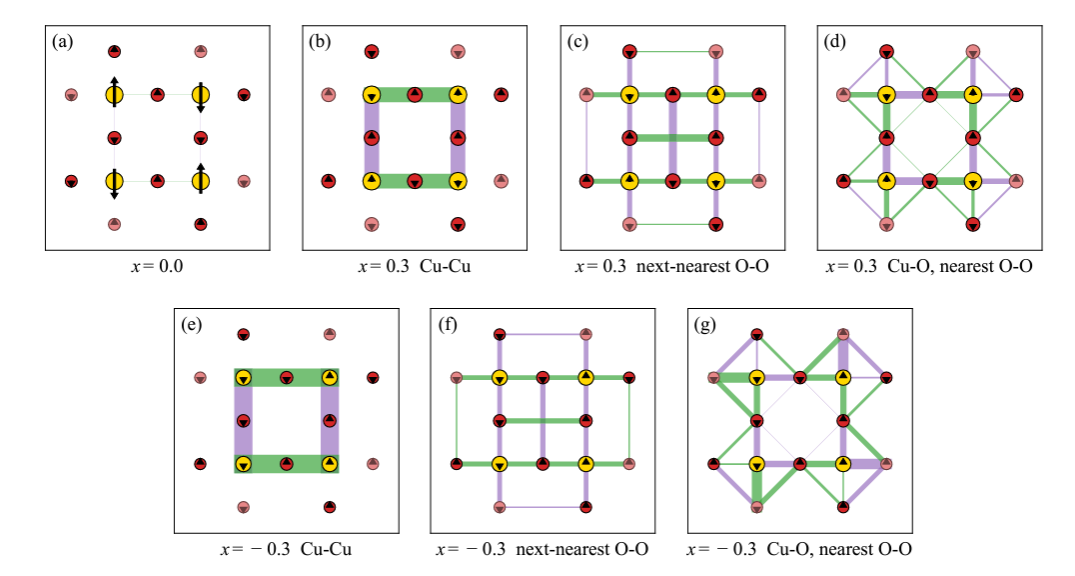
Three-band Hubbard model is a good model-approximation to the two-dimensional cuprate layer, which is the key structure of copper-based high-temperature superconductors. This paper applied density matrix embedding theory (DMET) to simulating the magnetic order and pairing parameters of the three-band Hubbard model with dopping, and shed light on understanding the mechanism of high Tc superconductors.

Monte-Carlo simulations of spin-crossover phenomena based on a vibronic Ising-like model with realistic parameters (Link)

H.-Z. Ye, C. Sun (Co-first Author) and H. Jiang. Phys. Chem. Chem. Phys. 17, 6801-6808 (2015).

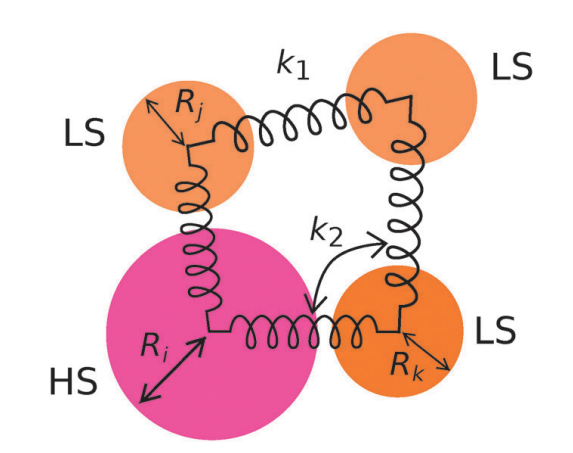
This work used realistic lattice parameters derived from density functional theory (DFT) simulations to study the spin crossover (SCO) behavior of the [Fe(pz)Pt(CN)4]·2H2O lattice. We simplified the complex lattice with an Ising-like model with elastic coupling between SCO centers. We profiled the thermal hysteresis of this SCO systems with Monte Carlo simulation.